减少层的“covariate shift”，提出Batch Normalization算法，大大改善了网络训练过程

神经网络训练原则是最小化loss函数，最常用的是mini-batch SGD。虽然SGD简单高效，但是它对调参要求很高，例如学习率以及参数初始化。每一个batch的数据，都是对整个训练集的估计；当输入改变，每一层的输出就会改变，即使前面层改变很小，经过几层处理，很可能放大这个变化。

输入层的改变，引起后面层的改变；这就要求层要不断适应新的数据分布。这种变化叫做“covariate shift”。

如果每层的输入分布都可以固定，那么训练神经网络将会变得简单。为了减少covariate shift，文章提出Batch Normalization算法；该算法不仅可以加速训练过程，还有利于梯度在网络间的传递（减小了梯度关于参数值大小的依赖）。Batch Normalization可以让网络使用更大的学习率，甚至不使用dropout。

Internal Covariate Shift是指网络中激活值得改变（因为神经网络训练过程中参数的改变）。如果可以固定每一层输入的分布，那么可以提升训练速度。例如，可以通过白化，固定好每一层输入的分布，这样就可以减少internal covariate shift带来的影响。

首先想到的是白化每层的激活值，1通过直接修改网络，2或改变激活值依赖的参数。但是这样的修改将会干扰优化算法，导致优化算法是按照Normalization来更新。

要确保对于任何参数值，网络的激活值总是服从期望分布。$x$是输入，$\chi$是整个训练集，那么normalization为：

$$
\hat x = Norm(x, \chi)
$$

不仅仅依赖$x$，还依赖$\chi$。反向传播还要计算

$$
\frac{\partial Norm(x,\chi)}{\partial x} \
\frac{\partial Norm(x,\chi)}{\partial \chi} \
$$

这样的话，白化每一层的输入，计算量很大，要计算

$$
Cov[x] = E_{x\in \chi}[xx^T] - E[x]E[x]^T \
Cov[x]^{-\frac{1}{2}}(x - E[x])
$$

还要计算它们的偏导。上面计算量太大，要寻找一种不需要在每次参数更新时都计算整个训练集的方法。

对整个训练集做Normalization，代价太大，一种容易想到的方法是对一个Mini-Batch做Normalization。一层的输入时d维$\text x = (x^{(1)} \cdots x^{(d)})$，对每一个维度做normalize

$$ {\hat x}^{(k)} = \frac{{\hat x}^{(k)} - E[{x}^{(k)}]}{\sqrt{Var[{x}^{(k)}]}} $$

通过上面的白化处理，可以改变数据分布，但是也改变了数据的表达能力。例如使用sigmod作为激活函数，白化操作会使数据分布在“0”附近，即在sigmod线性附近。为了确保变换是“表达能力”方面的等价变换，还要再每一维度引入缩放和平移参数：$\gamma^{(k)}, \beta ^{(k)}$

$$ y^{(k)} = \gamma^{(k)} {\hat x}^{(k)} + \beta ^{(k)} $$

这些参数和网络参数一起来学习获得，用来恢复网络表达能力。实际上如果$\gamma^{(k)} = \sqrt{Var[{x}^{(k)}]},\beta ^{(k)} = E[{x}^{(k)}] $就可以恢复出输入的原始值。

上面均值和方差，都是计算一个mini-batch数据获得的，而不是整个训练集。

假设一个mini-batch数据有$m$个，去一个维度的数据

$$ \beta = \{x_{1 \cdots m}\} $$

经过线性变换得到$y_{1 \cdots m}$，这个变化可以表示为：

$$ \textbf{BN}_{\gamma, \beta} : x_{1 \cdots m} \rightarrow y_{1 \cdots m} $$

下面就是Batch Normalization算法过程

假设$l$为loss，那么反向传播时，链式法则求导为：

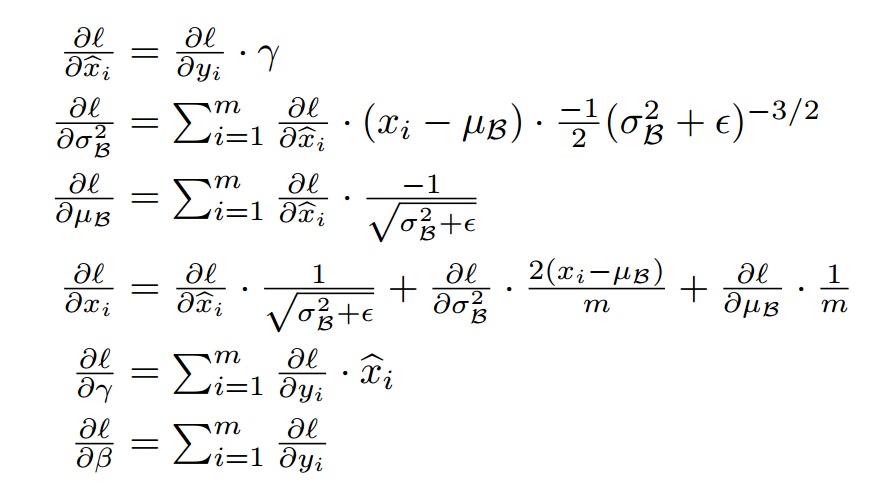
在训练时，使用mini-batch计算均值和方差，在intference时，就要使用无偏估计了，均值估计时无偏估计，但是方差不是，无偏估计的方差为：

$$ Var[x] = \frac{m}{m-1}E_{\beta}[\sigma^2_{\beta}] $$

最后可以得到一个完整的Batch Normalization算法